問題
一定の加速度で運動している物体Pがが点Oを東向きに速さ8m/sで通過し、7秒後に点Aを西向きに速さ6m/sで通過した。
(1)物体Pの加速度aを求めよ。
(2)点Oと点Aの距離lを求めよ。
(3)物体Pが点Oから最も離れた点Bと点Oの距離Lを求めよ。
まず、問題を解く前に
①与えられている状況の確認・類推
②与えられている数値の確認
を必ずすること。
物体Pは東向きに速さ8m/sで通過する ⇒
7秒後に ⇒
物体Pは西向きに速さ8m/sで通過する ⇒
[POINT]
最初の初速度の向きと、最後の速度の向きが異なる点に注目する。
初速度の向きを常にプラス正にとり、逆向きはマイナス負で表すことが大事!
(1) 公式  より、
より、
マイナスは「逆向き」という向きを示している
ゆえに、東向きに加速度
(2) 公式 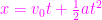 より、
より、
ゆえに、距離
(3) 物体は右向き8m/sから徐々に遅くなり、やがて向きを変え、西向き6m/sになる。
すなわち、最も離れた点では、物体の速度が0になっている。
この時の時間は与えられていないので、公式は 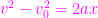 を用いる。。
を用いる。。
ゆえに、距離