◆
M:僕んち、エンゲル係数高いです。
T:突然やな。
M:エンゲル係数って知ってる?
T:家計の消費支出に占める食費のパーセントやろ?
M:そうです。そんな僕は、会社から給料をもらうと、その給料は貯金するか、食費になるかのどちらかです。しかも食事のカロリー係数が高いので、食費はすべて体重増加となります。
T:なんの話や?
M:すなわち、僕がもらった給料は、貯金増加か、体重増加になるわけです。
T:だから、なんの話やねん#
M:会社からもらう給料は、外部から得る熱量 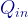 に似ています。
に似ています。
T:そうか?
M:給料の増加分は、内部エネルギーの増加  に似ています。
に似ています。
T:そうか?
M:ちなみに、内部エネルギーの増加は、内部温度の上昇を意味します。ほら、貯金するとうれしくて体温が上昇するのと同じ♪
T:あほか。
M:体重の増加分は、気体のした仕事 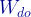 に似ています。だって、気体のした仕事は、内部の気体の体積増加を示すから♪ 体重増加と体積増加はまさにぴったり同じ♪
に似ています。だって、気体のした仕事は、内部の気体の体積増加を示すから♪ 体重増加と体積増加はまさにぴったり同じ♪
T:♪ マークやめろ。
M:そういうわけで、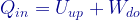 になるわけです。
になるわけです。
T:ん~、まぁまぁわかった。
M:さて、実際の問題としては、これに条件を付け加えます。
T:どんな?
M:たとえば、外界からの熱のやり取りを遮断する「断熱変化」。この場合は、外界から得る熱量がないので、 になります。
になります。
T:なるほど。
M:あるいは、内部温度を一定に保つ「等温変化」とかね。
T:その場合、内部温度の変化がないから、 やな。
やな。
M:そうそう。じゃぁ、「定積変化」の場合は?
T:「定積変化」って?
M:体積が一定という意味だよ。
T:ん~、体積一定なら、内部の気体が増加しないということだから、 や。
や。
M:そういうこと。その値を、さっきの、熱力学の第一法則「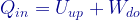 」にあてはめて考えれば、「等温変化」の場合は、外部から得た熱量がそのまま体積増加につながるということになる。
」にあてはめて考えれば、「等温変化」の場合は、外部から得た熱量がそのまま体積増加につながるということになる。
T:なるほどね。
M:では、「断熱変化」で、内部温度を上げたら?
T: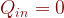 で、
で、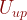 が正の値ならば、
が正の値ならば、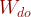 の値はマイナスになる
の値はマイナスになる
M:そうそう。
T: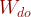 の値がマイナスということは、内部の気体の体積が減少するなぁ。
の値がマイナスということは、内部の気体の体積が減少するなぁ。
M:そうだね。
T:給料もらえんと、貯金もできんし、やせ細っていくゆうことか?
M:・・・・
